The game hexplode lets two players fight one another using exploding stacks of their tokens as means to take over enemy tokens. Over time, chain reactions become more and more common and as a result the game becomes difficult to predict. Here, I implement a ‘minimax’ algorithm to create a (very basic) computer player for this game. You can test your skills against it here

The Game

Hexplode is almost as old as space invaders. The game of was first created as a BASIC program for the BBC Micro written by J. Ansell in 1982. I started working on this game as part of the 2016 Man AHL coder prize. I am using their implementation here, which is openly available on GitHub. Their summary of the game is this:

Hexplode is played by 2 players on a board of hexagonal tiles. The players take turns to place a counter on the board, they can only play a counter in an empty tile or a tile they already own. When the number of counters on a given tile equals the number of adjacent tiles the tile hexplodes and the contents of the tile are equally distributed to its neighbours changing the ownership of neighbouring counters over to the current player in the process. This process can often generate a chain reaction. The winner is the player that removes all of their opponents counters from the board.

Man AHL ships their version with a flask app that allows us to run the game as a web server. This can be done either locally, or in the cloud. I have a version running on PythonAnywhere, which you can access at http://janlauge.pythonanywhere.com. Here is an example of what it looks like:

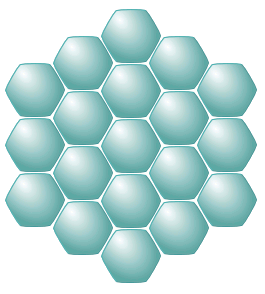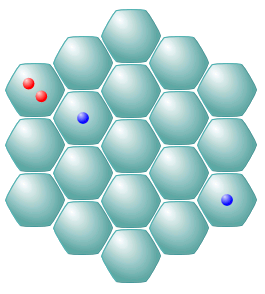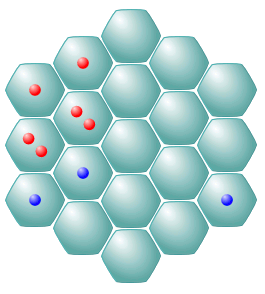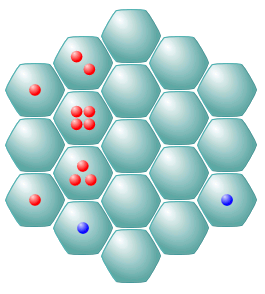
On the algorithm backend, the game is represented by a simple board state in the form of a python dictionary. Each tile has a tile_id, a score (the number of counters on that tile), an owner (the ID of the player that owns the token on this tile), and a list of neighbours indicated by their respective IDs.

board = {
    <tile id>: {
        'counters': <number of counters on tile or None>,
        'player': <player id of the player who holds the tile or None>,
        'neighbours': <list of ids of neighbouring tile>
    },
    ...
}

The Algorithm

In a game-theoretical sense, hexplode is an adversarial, deterministic game with perfect information. This means that the players are pursuing opposing goals, that there is no element of chance or randomness, and that all information about the state of the game world is always available to all players.

All three of these are attributes that hexplode shares with chess. I therefore decided to start my work on the competition with a ‘MiniMax’ implementation. This algorithm uses a tree approach. Each branch is a possible move, each leaf represents the resulting board state. Board states in terminal leaves are evaluated one by one, as “game over” for either player (+/- infinity), or, if that does not apply, using a heuristic value function (see diagram below).

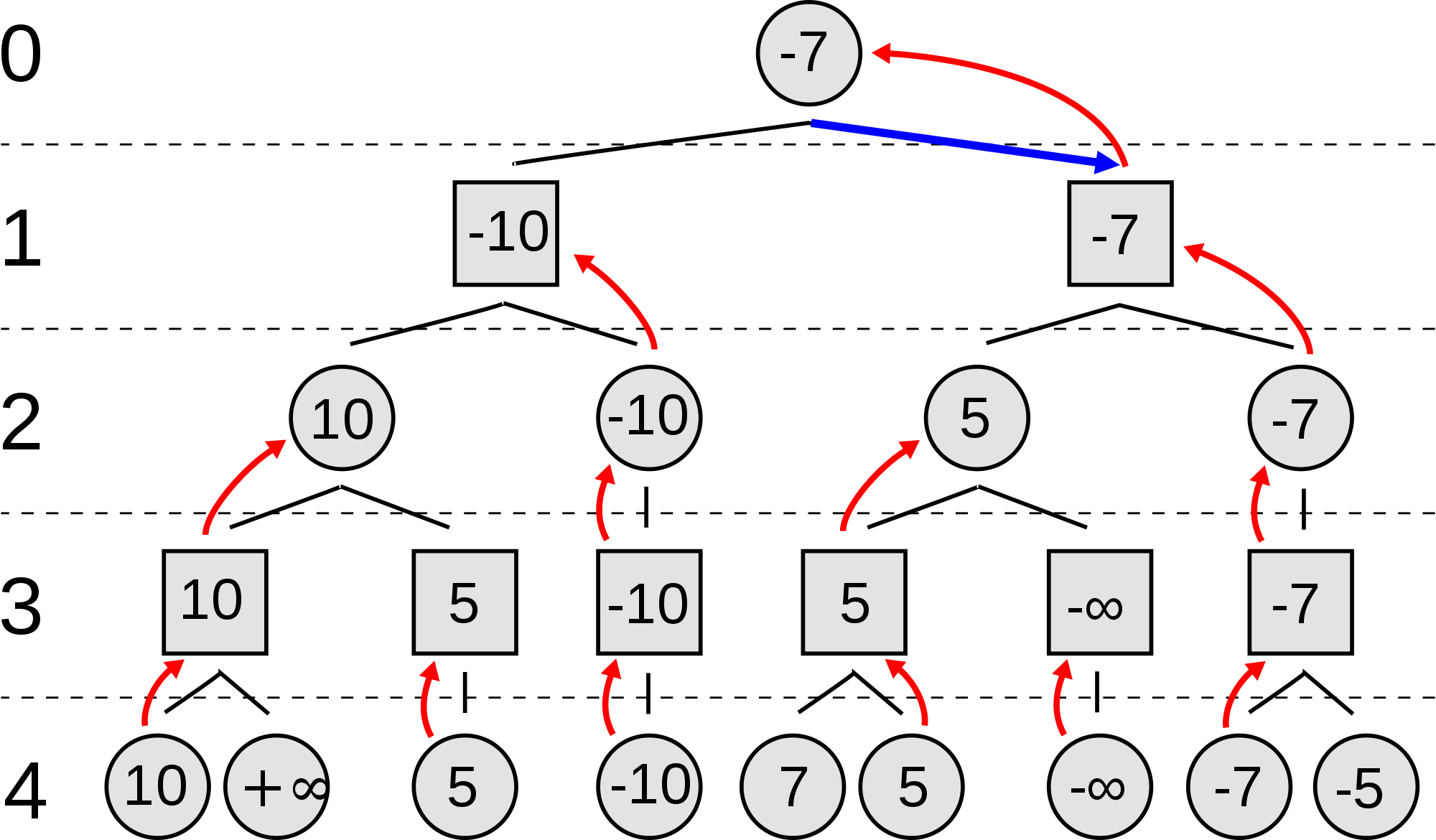source: Wikimedia commons

Board State

Minimax is relatively straight-forward to implement. First, we need to be able to calculate future board states as a function of our moves. We create a function AddCounter for this, which uses a list of scores, the board shape, the id of the tile that the counter should be placed on, along with the player_id (the algorithm) and the current player (the one placing the counter, because we want to be able to simulate enemy moves as well). Note that this is a recursive function, because placing a marker on a tile can create an instable board state with as many counters on a tile as that tile has neighbours. In this case, the tile will “hexplode”, distributing its counters to the neighbouring tiles. This, in turn, could trigger subsequent hexplodes on those neighbouring tiles, which would be handled by the respective recursions triggered by the function.

def AddCounter(scores, board, tile_id, player_id, player_current):
    if (True in [score > 0 for score in scores.values()]) and (True in [score < 0 for score in scores.values()]):
        #If player, counters are positive
        if player_current == player_id:
            add = +1
        #If enemy, counters are negative
        else:
            add = -1
        #If placing counter on own tile, increase counters
        if (add > 0 and scores[tile_id] >= 0) or (add < 0 and scores[tile_id] <= 0):
            counter = scores[tile_id] + add
        #If placing counter on enemy tile, change and increase counters
        else:
            counter = (scores[tile_id] * -1) + add
        #If field full, hexplode (recursive)
        if abs(counter) == len(board[tile_id]["neighbours"]):
            scores[tile_id] = 0
            for neighbour in board[tile_id]["neighbours"]:
                scores = AddCounter(scores, board, neighbour, player_id, player_current)
        else:
            scores[tile_id] = counter
        return(scores)
    else:
        return(scores)

Growing Trees

Now that we can calculate and evaluate potential future board states, we can use this to create a tree of move scenarios. A given board state allows for a number of moves (“place a marker on any tile that is not an enemy tile”). When it is our turn, we can make n_1 valid moves resulting in n_1 possible board states. Using another recursion call we can calculate n_2 valid enemy moves with termination conditions for a maximum depth (n_i) and/or for a game-over situation (one player looses all counters).

class Node(object):

    def __init__(self, board, player_id, player_current, scores, depth, move=None):
        self.player_current = player_current
        self.move = move
        self.scores = scores

        #Check if game is over
        if (True in [score > 0 for score in self.scores.values()]) and (True in [score < 0 for score in self.scores.values()]):
            self.depth = depth
        else:
            self.depth = 0

        #If this is not a terminal node, generate the children
        if self.depth > 0:
            #Prefix for use with score
            if (self.player_current == player_id):
                self.prefix = 1
            else:
                self.prefix = -1
            self.children = []
            self.CreateChildren(scores)

        #If this is terminal node, calculate value
        elif self.depth == 0:
            #Get Value
            self.value = CalculateValue(scores, player_id)

    def CreateChildren(self, scores):
        for tile_id in scores.keys():
            if ((scores[tile_id] >= 0) and (self.prefix > 0)) or ((scores[tile_id] <= 0) and (self.prefix < 0)):
                future_scores = copy(scores)
                future_scores = AddCounter(future_scores, board, tile_id, player_id, self.player_current)
                self.children.append(Node(
                    board,
                    player_id,
                    (self.player_current + 1) % 2,
                    future_scores,
                    self.depth -1,
                    tile_id))

Adding Value

So we have our tree of all possible future board configurations now. However, how do we actually figure out which one is the most favourable or the most likely scenario? This is where the Minimax algorithm comes into play. Let’s assume for a second that we grew trees indefinitely, until each branch reaches a “game-over” state where all counters belong to one player. Furthermore, let’s say that we will assign a value to each of those terminal branches: Inf (positive infinity) for a branch in which we win, -Inf (negative infinity) for a branch in which we loose.

In reality, however, we will not be able to calculate all terminal nodes. Consider this: A hexagonal board of side length 3 will have 19 tiles, equating to 19 possible moves in the first round. Each of these results in a board state with 18 possible moves for the enemy (361 board states in total), then 18 for us again (6517 board states in total), and so on and so forth. This quickly gets out of hand. We somehow need to keep the number of board states manageable.

One way to achieve this is to limit the depth of our tree and evaluate the “favourability” of each terminal leaf using a heuristic value function. In this example, let’s go for something simple, such as the number of markers that we have on the board, minus the number of enemy markers. If for a given board state we’re in the lead, the number will be positive. If we’re behind, the number will be negative.

def CalculateScores(board, player_id):
    scores = {}
    for tile_id, tile in board.items():
        if tile["player"] == None:
            scores[tile_id] = 0
        elif tile["player"] == player_id:
            scores[tile_id] = int(tile["counters"])
        elif tile["player"] is not player_id:
            scores[tile_id] = int(tile["counters"]) * -1
    return(scores)


def CalculateValue(scores, player_id):
    """Heuristic value function to estimate how favourable
    the given board state is for the player"""

    # count counters
    OwnCounters = 0
    EnemyCounters = 0
    for tile_id in scores:
        if scores[tile_id] > 0:
            OwnCounters += abs(scores[tile_id])
        elif scores[tile_id] < 0:
            EnemyCounters += abs(scores[tile_id])
    # Check for game-over
    if OwnCounters == 0:
        #Lost
        return(-maxsize)
    elif EnemyCounters == 0:
        #Won
        return(maxsize)
    else:
        value = OwnCounters - EnemyCounters
        return(value)

We can “back-propagate” these outcomes up the tree and assume that each player will always pick the move that will bring them closer towards a winning branch rather than a loosing branch. In other words, we will try to maximise the value, our enemy will try to minimize it. Since we take turns at the moves, it becomes Max, Min, Max, Min, ergo MiniMax. This can be coded up with yet another recursive approach. This time we use two functions that call one-another, and take the node tree object we created as an input variable.

def Maxvalue(node):
    """Function to identify most advantageous player move"""
    if (node.depth == 0):
        return node.value
    else:
        best_value = -maxsize
        for child in node.children:
            best_value = max(best_value, Minvalue(child))
        return best_value

def Minvalue(node):
    """Function to identify most likely enemy move"""
    if (node.depth == 0):
        return node.value
    else:
        best_value = maxsize
        for child in node.children:
            best_value = min(best_value, Maxvalue(child))
        return best_value

Putting it all Together

Finally, we can join up all these individual parts and make them talk to the web app. The Minimax function below takes the inputs board, game_id and player_id from the flask app hosting the game, calculates the future possible board states by instanciating a Node object, and then picks the most favourable move from all moves currently possible by evaluating the future scenarios.

def Minimax(board, game_id, player_id):

  # Run algorithm
  depth = 3
  scores = CalculateScores(board, player_id)
  moves = sum([abs(score) for score in scores.values()])

  # If the game is only starting, pick first tile
  if moves < 2:
      possible_moves = {}
      for tile_id, tile in board.items():
          if tile["player"] is None:
              possible_moves.setdefault(len(tile["neighbours"]), []).append(tile_id)
      # Pick the moves closest to an explosion
      best_move = possible_moves[min(possible_moves)][2]

      return best_move

  else:
      node_tree = Node(board, player_id, player_id, scores, depth)
      candidate_moves = {}
      for child in node_tree.children:
          candidate_moves[child.move] = Minvalue(child)
      best_move = max(candidate_moves.keys(), key=(lambda k: candidate_moves[k]))

      return best_move

I’ve included this function in my version of the web app running on pythonanywhere, so head over there and give it a go! http://janlauge.pythonanywhere.com

I hope this is mildly interesting and/or useful. I’d be glad for any feedback on my approach, the code (this was one of my first projects in python), and this post in general. Thanks to Man AHL for hosting this interesting challenge!